Recording Magazine sends out a newsletter to its subscribers every few weeks. The newsletter is (coincidentally) titled “Sound Advice” and this month it features the second in a series about room acoustics. As you will read, room acoustics is one of the biggest concerns for Recording Magazine readers. I know that this is also a big issue for those of you in the voiceover world. Like I did last month, I asked permission to reprint the series (and will ask to reprint the others in the series as well) so that those of you with home studios can also benefit from the information. I want to personally thank Brent Heintz, VP/Associate Publisher for granting permission, allowing me to share this great information with you.
Please visit Recording Magazine‘s website and their Facebook Page.
Catch up or skip ahead: Part 1, Part 3, Part 4, Part 5, Part 6, Part 7, Part 8.
Here is the second newsletter in the series on Room Acoustics:
Welcome to Sound Advice on Acoustics! Last time we sketched out the basic properties of sound: amplitude, frequency, and wavelength. And we talked about how sound waves in air interact with one another to make certain frequencies louder and others softer at various places in the room. Armed with those basic terms and ideas, it’s time for us to look at some real-world problems…
Low-frequency energy that is unevenly distributed is one of the main problems. When you apply the wavelength formula you’ll see that the wavelengths of bass notes easily exceed the measurements of typical rooms. Example: 55 Hz (the open A string on a bass) works out as follows: 1130 ÷ 55 = 20.54 feet. Few control rooms are deeper than 20’6″. When long waves approach and exceed the dimensions of the room, they are forced to fold back onto themselves, and the resulting cancellations and reinforcements will be localized to specific areas in the room. This results in clearly audible artifacts that must be dealt with. Fortunately, these interferences can be calculated and mapped out in the room.
In analyzing a room, the first aspect to consider is its overall size, as this will determine the limit of low-frequency support. Frequencies whose wavelengths are longer than half the longest dimension in a room are said to be unsupported in that room.
Take a small room with dimensions of 1’L x 10’W x 8’H. The formula 1130 ÷ 2L (where 1130 = the speed of sound in feet/sec, and 2L = the longest room dimension multiplied by two) gives us the lowest supported frequency in that room: 1130 ÷ 24 = 47.08, about 47 Hz (for reference, the fundamental of the lowest note on a 4-string bass is about 42 Hz). Frequencies below this will be unsupported, which doesn’t mean that they can’t exist in that room, but that they will be weaker from lack of resonant support (reinforcement by room resonances).
A special problem occurs with the frequency whose wavelength is exactly 1130 ÷ 2L; this will produce what’s called a standing wave or mode. This is a room resonance that occurs when a wave reflects between two parallel surfaces in the room. As the wave is contained by the room, a stationary distribution of reinforcements (boosts in level) and cancellations (null points) will be established as shown in Figure 1A.
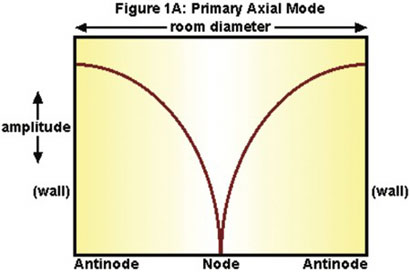
The reinforcements (maximum pressure) of the standing wave occur at the walls (the points of reflection), while a cancellation occurs midway between the walls. This happens between every pair of parallel walls in the room (there are three pairs in a rectangular room, front/rear walls, side walls, and floor/ceiling).
The locations in the room where the sound wave is canceled are called nodes (in this example the midway point); the areas of maximum reinforcement are called antinodes (in this example at the walls). If you generated a sine wave test tone at that frequency, stood at one wall, and slowly walked to the other wall, you would hear that tone drop in level as you passed the midway point and increase in level again as you approached the opposite wall.
So far we’ve established the first modal frequency in that room, and obviously there are at least three, one for each pair of parallel surfaces. That’s only the beginning—for each room dimension, there are additional modal frequencies.
The second harmonic of this first mode will be twice that frequency and therefore half the wavelength—a sound wave of this frequency will also form a standing wave with discrete node and antinode areas. Since the wavelength of the second harmonic is half that of the fundamental’s, the peaks and nulls will be more closely spaced (by half), as illustrated in Figure 1B.
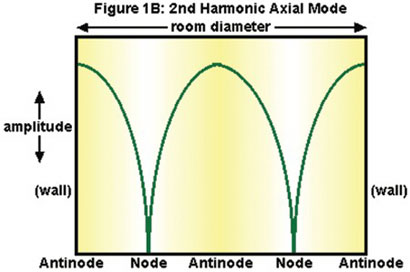
Once again (as always), the standing wave’s reinforcements occur at the walls, but now another reinforcement (Antinode) occurs halfway between, with cancellations (Nodes) a quarter of the way out from each wall. Again, remember this happens for each of the three parallel surfaces in the room.
The same effect happens at the third harmonic (3 x the frequency, 1/3 the wavelength) of that initial modal frequency, (Figure 1C), and so on up, with more closely spaced nodes and antinodes. Eventually the wavelengths will become short enough that the reduced strength, greater density, and closer spacing of the various nodes and antinodes will tend to average out rather than be audible at specific spots in the room; this will happen gradually, beginning at around 300–400 Hz.
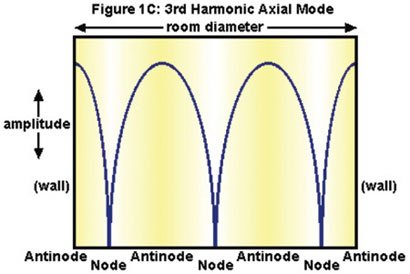
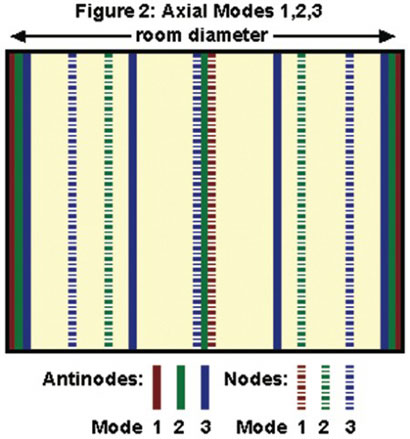
Figure 2 shows a plot of where the nodes and antinodes of the first three of these modes occur in the room. If you plotted each of the three pairs of parallel surfaces and overlaid them, you’d see the specific layout and intersections of the various nodes and antinodes. The particular frequencies affected would of course depend on the room dimensions.
And that’s not all—the modes described so far are only one of three types that exist in any rectangular room. These modes, which occur between two parallel surfaces, are called axial modes. They are by far the strongest and most problematic, but they’re not alone. Standing waves also result when sound waves bounce around four surfaces (see Figure 3)—these are called tangential modes; they have half the energy of the axial modes. Finally, oblique modes arise from sound waves that bounce around all six surfaces; these have one-quarter the energy of the axial modes.
There will always be a buildup of bass at each wall, and in the corners, where the different modes intersect, generating even more low-frequency energy; the three-way intersection of two walls and ceiling or floor will have the greatest amount of low-end buildup.
To fully analyze the low-frequency behavior in a room, all of these modes would have to be calculated and mapped out, but this is difficult to do without test equipment, and since the axial modes are by far the most prominent, we’ll focus on those to create some representative charts of modal behavior in typical rooms. We’ll do that next time… see you then!



